* EXCERPT: The concept of angle is one of the most important concepts in geometry. The concepts of equality, sums, and differences of angles are important and used throughout geometry, but the subject of trigonometry is based on the measurement of angles.

There are two commonly used units of measurement for angles. The more familiar unit of measurement is that of degrees. A circle is divided into 360 equal degrees, so that a right angle is 90°... Degrees may be further divided into minutes and seconds, but that division is not as universal as it used to be. Parts of a degree are now frequently referred to decimally. For instance seven and a half degrees is now usually written 7.5°. Each degree is divided into 60 equal parts called minutes. So seven and a half degrees can be called 7 degrees and 30 minutes, written 7° 30'. Each minute is further divided into 60 equal parts called seconds, and, for instance, 2 degrees 5 minutes 30 seconds is written 2° 5' 30". The division of degrees into minutes and seconds of angle is analogous to the division of hours into minutes and seconds of time.

Usually when a single angle is drawn on a xy-plane for analysis, we'll draw it with the vertex at the origin (0,0), one side of the angle along the x-axis, and the other side above the x-axis.

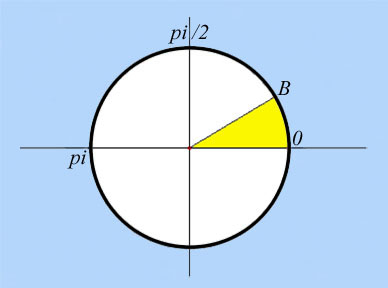
The other common measurement for angles is radians. For this measurement, consider the unit circle (a circle of radius 1) whose center is the vertex of the angle in question. Then the angle cuts off an arc of the circle, and the length of that arc is the radian measure of the angle. It is easy to convert between degree measurement and radian measurement. The circumference of the entire circle is 2pi (pi is about 3.14159), so it follows that 360° equals 2pi radians. Hence, 1° equals pi/180 radians, and 1 radian equals 180/pi degrees.

Although the word "radian" was coined by Thomas Muir and/or James Thompson about 1870, mathematicians had been measuring angles that way for a long time. For instance, Leonhard Euler (1707-1783) in his Elements of Algebra explicitly said to measure angles by the length of the arc cut off in the unit circle. That was necessary to give his famous formula involving complex numbers that relates the sign and cosine functions to the exponential function where t is what was later called the radian measurment of the angle.

Radians and arc length: An alternate definition of radians is sometimes given as a ratio. Instead of taking the unit circle with center at the vertex of the angle, take any circle with center at the vertex of the angle. Then the radian measure of the angle is the ratio of the length of the subtended arc to the radius of the circle. For instance, if the length of the arc is 3 and the radius of the circle is 2, then the radian measure is 1.5. The reason that this definition works is that the length of the subtended arc is proportional to the radius of the circle. In particular, the definition in terms of a ratio gives the same figure as that given above using the unit circle. This alternate definition is more useful, however, since you can use it to relate lengths of arcs to angles. The formula for this relation is radian measure times radius = arc length. For instance, an arc of 0.3 radians in a circle of radius 4 has length 0.3 times 4, that is, 1.2. * END EXCERPT *

According to the Zodiac's instructions, his code and map clues concerned "radians and # inches along the radians."

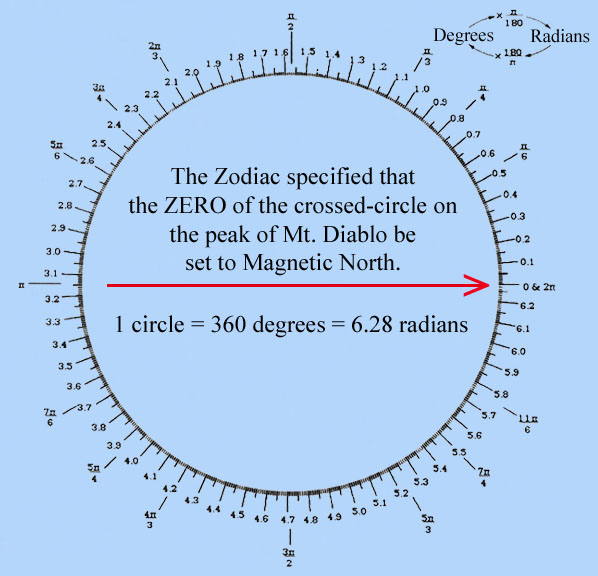
The Zodiac also stated that the ZERO of the crossed-circle on the peak of Mt. Diablo was to be "set" to Magnetic North. The illustration below demonstrates the results achieved when following the Zodiac's instructions. The number of radians along the circumference of the circle are represented in red.

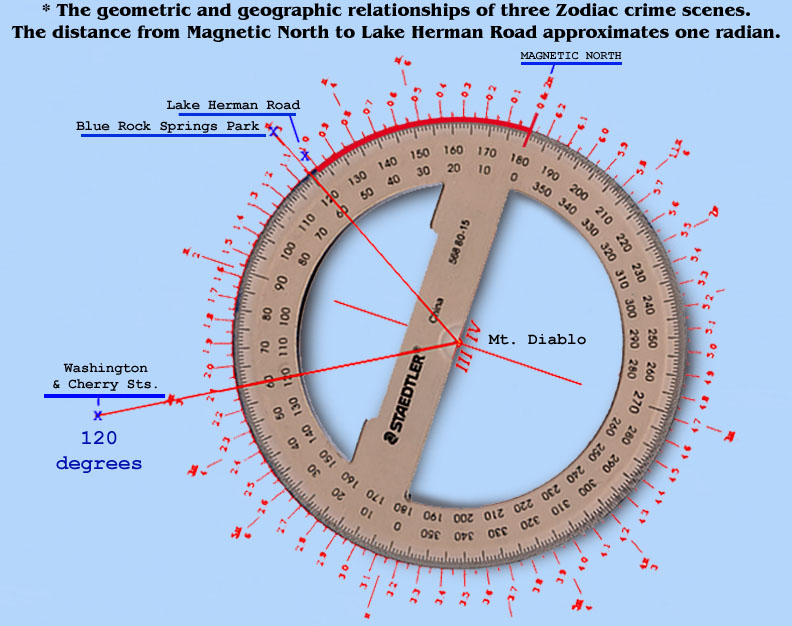
The geographic and geometric relationships created by the Zodiac locations and Mt. Diablo is not an interpretation or a theory but an undeniable fact. One may be tempted to dismiss these alignments as coincidence if the Zodiac had not sent a map with a crossed-circle on the peak of the one major benchmark in Northern California and cited instructions regarding radians and inches. The Zodiac claimed that the code which accompanied the map and letter would provide the information needed to identify and find a specific location. Until the code is deciphered, no one can know the Zodiac's true intentions but the alignments created by the scenes he chose to mark with murder indicates that these geographic and geometric relationships may be the product of deliberate design.